Higher polynomials

$ax^{n}+bx^{n-\Delta }+cx^{n-\Delta {_{1}}}+\sum _{k=\alpha {_{1}}}^{\alpha {_{n-3}}}x^{k-\Delta }\alpha =0$

Здесь приведены основные способы решений частных уравнений выше четвёртой степени. Нахождение корней у многочленов степени выше чем 4, всегда являлось проблемой. Много лет было потрачено на нахождение общей формулы кубических уравнений, но уравнения имеющие показатель выше четырёх были описаны в теории Абеля, как неразрешимые. Далеко канешно не все из них является такими, говорил Абель. Многие уравнения в этой статье являются особенными исключениями из большого множества подобных уравнений, потому-что в них используются минимум дополнительных слагаемых и изменений в коэффициентах.

Решение уравнения шестой степени в частных радикалах:[править]

ax^{6}+bx^{5}+cx^{4}+dx^{3}+ex^{2}+fx+g+v=0,\quad a\neq 0.

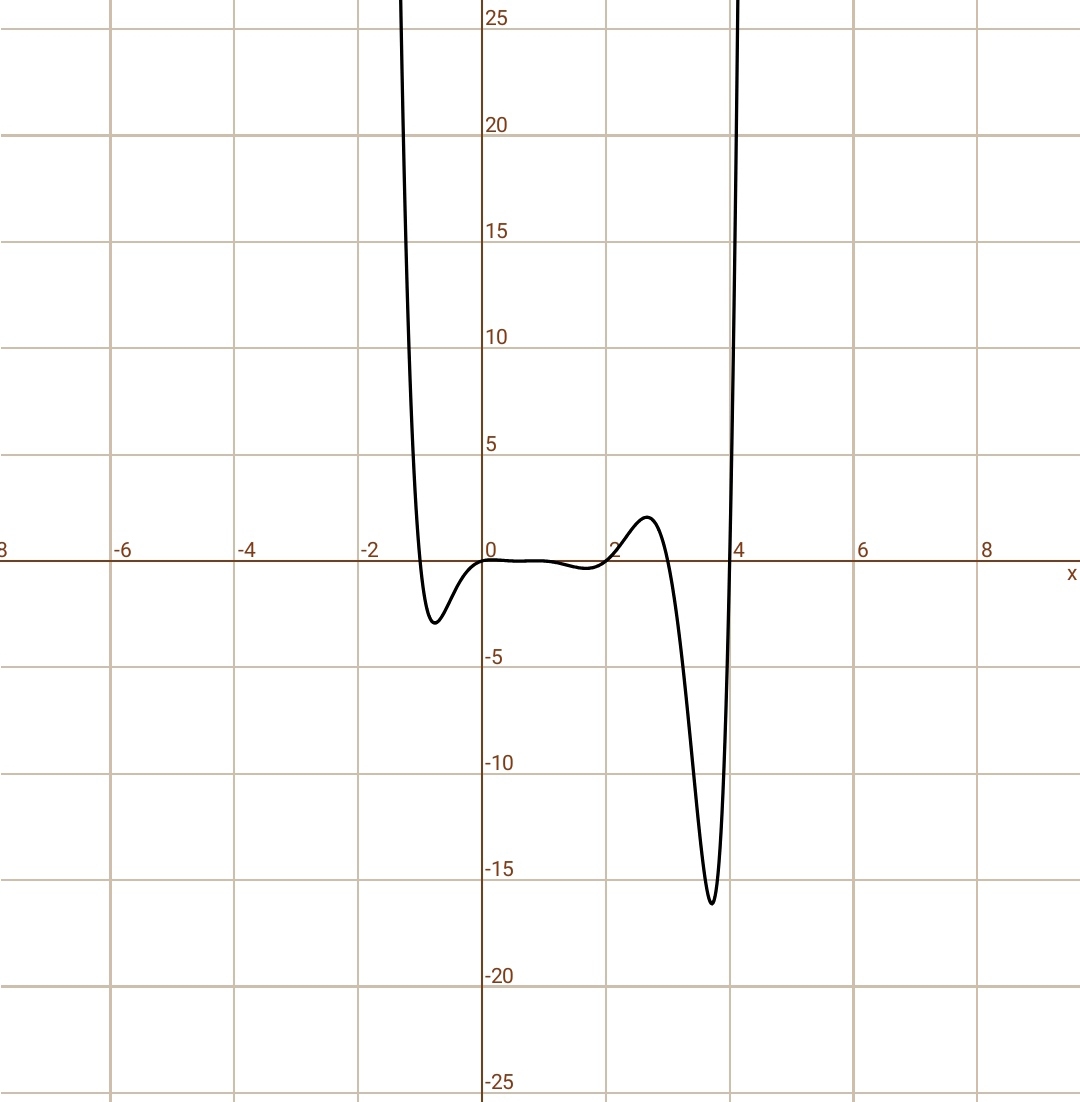
Вид графика:

graph

Уравнения такого вида является разрешимым в аналитических радикалах, только тогда когда $v,\quad a\neq 0.$ является параметром, имеющий фиксированное значение. Его можно вычислить по [1] кубического уравнения с четырьмя уравнениями в системе. При этом остальные коэффициенты останутся неизменными.

{\begin{cases}2a+2b=-{\dfrac {2t}{p}},\\(a+b)^{2}+2ab={\dfrac {r}{p}},\\2ab(a+b)={\dfrac {w}{p}},\\(a^{2})(b^{2})={\dfrac {n}{p}},+{\dfrac {v}{ap}},-{\dfrac {q^{2}}{4p}}-{\dfrac {t^{2}}{p}}-{\dfrac {qt}{p}},\\\end{cases}}

Для того чтобы найти коэффициенты $p,q,r,w,n$ Необходимо убрать коэффициент $bx^{5}$ При помощи выделения полной шестой степени, можем выразить значения коэффициентов, где:

$p={\dfrac {12ac-5b^{2}}{12a^{2}}}$ $q={\dfrac {27a^{2}d+5b^{3}-18abc}{27a^{3}}}$ $r={\dfrac {24acb^{2}-5b^{4}-72bda^{2}-144ea^{3}}{144a^{4}}}$ $w={\dfrac {-6ab^{3}c+27da^{2}b^{2}-108ea^{3}b+b^{5}+324a^{4}f}{324a^{5}}}$ $n={\dfrac {46656a^{5}g+36ab^{4}c-5b^{6}-216a^{2}b^{3}d+1296ea^{3}b^{2}-7776a^{4}bf}{46656a^{6}}}$ Для следующего вида уравнения: $y^{6}+py^{4}+qy^{3}+ry^{2}+wy+n+{\dfrac {v}{a}}=0,\quad a\neq 0.$ Для которого $x=y-{\dfrac {b}{6a}}$ . Распределим слагаемые в разных частях уравнения.

 $y^{6}+qy^{3}=-py^{4}-ry^{2}-wy-n-{\dfrac {v}{a}}$

Также добавим к обеим частям $+{\dfrac {q^{2}}{4}}$ для того чтобы снова получить полный квадрат. По итогу получим: $(y^{3}+{\dfrac {q}{2}})^{2}=-py^{4}-ry^{2}-wy-n-{\dfrac {v}{a}}+{\dfrac {q^{2}}{4}}$ Добавим в полный квадрат параметр: $t$ тогда соответственно добавим справа ещё 3 слагаемых: $t^{2},qt,2ty^{3}.$ По вследствие мы получили такое уравнение: $(y^{3}+{\dfrac {q}{2}}+t)^{2}=-py^{4}+2ty^{3}-ry^{2}-wy-n-{\dfrac {v}{a}}+{\dfrac {q^{2}}{4}}+qt+t^{2}$ Система которую мы записали характерна для следующего разложения. Коэффициенты a;b в системе являются корнями, такого многочлена: $(x+a)^{2}(x+b)^{2}=x^{4}+(2b+2a)x^{3}+(a^{2}+4ab+b^{2})x^{2}+(2a^{2}b+2b^{2}a)x+b^{2}a^{2}$ Из которых соответственно выходит данная система для такого уравнения: $-py^{4}+2ty^{3}-ry^{2}-wy-n-qt-t^{2}-{\dfrac {v}{a}}+{\dfrac {q^{2}}{4}}$ где находятся два параметра $t$ — является независимым параметром, а $v$ предстоит выразить для общего случая.

{\begin{cases}2a+2b=-{\dfrac {2t}{p}},\\(a+b)^{2}+2ab={\dfrac {r}{p}},\\2ab(a+b)={\dfrac {w}{p}},\\(a^{2})(b^{2})={\dfrac {n}{p}}+{\dfrac {v}{ap}}-{\dfrac {q^{2}}{4p}}-{\dfrac {t^{2}}{p}}-{\dfrac {qt}{p}},\\\end{cases}}

В первую очередь найдём значения $t,v$ они равны следующим значениям: $t=-p(a+b)$ и $v=a'p'(a^{2}b^{2}-{\dfrac {n}{p}}+{\dfrac {q^{2}}{4p}}+{\dfrac {t^{2}}{p}}+{\dfrac {qt}{p}})$ Оставшиеся корни a;b запишем в систему с заменой:

{\begin{cases}(a+b)^{2}+2ab={\dfrac {r}{p}},\\2ab(a+b)={\dfrac {w}{p}},\\\end{cases}}

При помощи замен выразим, $ab=u$ и $a+b=j$ Тогда: $ab={\dfrac {r}{2p}}-{\dfrac {(Z_{(}1,2,3))^{2}}{2}}.....a+b=Z_{(}1,2,3)$ Где Z(1,2,3) - это корни кубического уравнения вида: $-j^{3}+{\dfrac {r}{p}}j-{\dfrac {w}{p}}=0$ После каноничного раскрытия системы находим различные a и b (можно брать повторные) $b={\dfrac {Z(1,2,3)}{2}}+{\dfrac {\sqrt {(3pz(1,2,3)^{2}-2r)}}{2{\sqrt {(p)}}}}$ значение "a" просто вычитается перед радикалом. Root - квадратный корень. Найдем величины $a+b,ab,a^{2}b^{2}$ Первая) $a+b=Z(1,2,3)$ вторая) $ab={\dfrac {-pZ(1,2,3)^{2}+r}{2p}}$ Третья) $a^{2}b^{2}={\dfrac {r^{2}-2prZ(1,2,3)^{2}+p^{2}Z(1,2,3)^{4}}{4p^{2}}}$ По итогу получаем такое уравнение: $(y^{3}+{\dfrac {q}{2}}+t)^{2}=-p(x+a)^{2}(x+b)^{2}$ Которое можно свести к кубическому при помощи извлечения квадратного корня. $y^{3}-{\sqrt {p}}y^{2}i-{\sqrt {p}}(Z(1,2,3))yi-{\dfrac {-pZ(1,2,3)^{2}+r}{2p}}{\sqrt {p}}i+{\dfrac {q}{2}}+pZ(1,2,3)=0$ Которое как раз даёт ещё дополнительные 3 корня квинтики. $y_{1}+-y_{2}+-y_{3}$ Дополнительная распаковка даст ещё 3 би-корня зависящих от $Z_{1}+-Z_{2}+-Z_{3}$ И перестановки $a,b$ дадут ещё два возможных корня.

В упрощённом виде, формула для корня такого уравнения запишется следущим путём:

$y^{6}+py^{4}+qy^{3}+ry^{2}+\omega y+n+{\dfrac {v}{a}}$

$v={\dfrac {r^{2}}{4p}}a-na+a{\dfrac {q^{2}}{4}}+ap({\sqrt[{3}]{-{\dfrac {r}{2p}}+{\sqrt {{\dfrac {r^{2}}{4p^{2}}}-{\dfrac {w^{3}}{27p^{3}}}}}}}+{\sqrt[{3}]{-{\dfrac {r}{2p}}-{\sqrt {{\dfrac {r^{2}}{4p^{2}}}-{\dfrac {w^{3}}{27p^{3}}}}}}})(-q-(p+{\dfrac {r}{2p}})Z_{1,2,3}+0,25Z_{1,2,3}^{3})$

Если мы нашли "v" , то корень такого полинома, в упрощённом виде равен:

$x+{\dfrac {b}{6a}}={\sqrt[{3}]{-{\dfrac {-pZ_{1,2,3}^{2}}{4p}}{\sqrt {p}}i-0,25q-0,5Z_{1,2,3}+{\dfrac {pZ_{1,3,2}}{6}}+{\dfrac {-{\sqrt {p^{3}}}i}{54}}+{\sqrt {({\dfrac {-pZ_{1,2,3}^{2}-...}{2}})^{2}+({\dfrac {-3pZ_{1,2,3}-p}{12}})^{3}}}}}+{\sqrt[{3}]{...-{\sqrt {...}}}}+{\dfrac {{\sqrt {p}}i}{6}}$

= $ax^{6}+bx^{5}+cx^{4}+dx^{3}+ex^{2}+fx+g+a({\sqrt[{3}]{..+{\sqrt {...}}}}+\Delta )$ При перемножении всех шести корней получим такой полином.

Уравнение восьмой степени, частные случаи[править]

$ax^{8}+bx^{7}+cx^{6}+dx^{5}+ex^{4}+fx^{3}+gx^{2}+hx+j=0$ Если $a\neq 0$

graph

Существует достаточно много частных допустимых случаев, которые допускают аналитическое решение в радикалах.

Если: $b=0$ , $d=0$ , $f=0$ , $h=0$

То уравнения сводится к решению, би-уравнения четвёртой степени.

$ax^{8}+cx^{6}+ex^{4}+gx^{2}+j$

Корни которого можно получить по формуле Феррари:

$\pm {\sqrt {{\sqrt {y{_{1}}}}\pm {\sqrt {y{_{2}}}}\pm {\sqrt {y{_{3}}}}\pm {\sqrt {y{_{4}}}}}}={\dfrac {p}{8}}$

• Второй случай для биби-квадратного уравнения:

$ax^{8}+ex^{4}+j=0$

то корни такого уравнения выражаются по следующим формулам:

$x_{1,2,3,4}=\pm {\sqrt[{4}]{\dfrac {-e\pm {\sqrt {e^{2}-4aj}}}{2a}}}$

$x_{5,6,7,8}=\pm {\sqrt[{4}]{\dfrac {-e\pm {\sqrt {e^{2}-4aj}}}{2a}}}i$

• Третий случай.

Если $j=0$ то уравнения сводится к более простому ввиду:

$x(ax^{7}+bx^{6}+cx^{5}+dx^{4}+ex^{3}+fx^{2}+gx+h)$

Корни подобного уравнения пока-что общем виде нельзя выразить, но если окажется что "g" является параметром и $h=0$ то такое уравнение станет разрешимым в аналитических радикалах (1 категория←принцип решения).

• Четвертый случай.

Если уравнения восьмой степени имеет любые произвольные параметры, минимум на 2 коэффициентах, то данное можно свести к общему виду шестой степени:

Оно также рассматривает все частные случаи коэффициентов, подобных разрешимых уравнений.

$ax^{8}+bx^{7}+cx^{6}+dx^{5}+ex^{4}+fx^{3}+gx^{2}+(h+\theta {_{1}})x+g+\theta$ При помощи алгоритма разбиения на скобки квадратов (описанного выше) . Сведем к системе в которой окажется уравнения шестой степени: $x^{6}+\Delta {_{1}}x^{5}+\Delta {_{2}}x^{4}+\Delta {_{3}}x^{3}+\Delta {_{4}}x^{2}+\Delta {_{5}}x+\Delta {_{6}}=0$

К сожалению в общем виде, это уравнение также не разрешимо, поэтому $\Delta {_{6}}$ должно иметь особенное значение, что дабавляет параметр в общий вид. Из чего следует, что количество параметров необходимых для разрешимости определяет формула: $n-5$ . Где n - степень полинома. Очень быстро появится следующий вопрос, почему тогда полином пятой степени, не является разрешимым видь количество коэффициентов равно 5. В теории Абеля кратко описывается данный феномен. Особенность стоит в корне ${\sqrt[{5}]{Z}}$ . Если рассматривать кубическое уравнение, то в нём используется нечётная степень корня. А уравнение четвертой степени будто обходит корень четвёртой степени. Потому-что его можно разбить на два квадратных корня. Секрет разрешимости состоит как раз в этом особенном преобразования что шестая степень образуется из групп [2×3](квадратного и кубического радикала), но из-за снижения поля ему потребуется пройти через радикал пятой степени. Параметр $v$ позволяет обойти это. Он находит такую особенную перестановку, которая удаляет корень пятой степени. Тем самым разбивая группы на более простые. Пока-что выразить все параметры невозможно из-за ограничений размеров редактора и в сложности их нахождения.

• Пятый случай.

Если коэффициенты повторяются, то можно сделать группировку например:

$ax^{8}+bx^{7}+cx^{6}+dx^{5}+ax^{4}+bx^{3}+cx^{2}+dx^{1}$

Первый корень: x=0 Дальше выносим:

$x(ax^{3}+bx^{2}+cx+d)(x^{4}+1)$

Где все корни можно найти не превышая кубическое уравнение.

Ряд сходимости уравнений в разрешимых частных радикалах[править]

$(x^{2}+ax+b)(x^{4}+dx^{2}+e)(x^{6}+fx^{4}+g)(x^{8}+hx^{4}+k)(x^{10}+qx^{5}+w)(x^{12}+rx^{6}+t)(x^{16}+yx^{8}+u)(x^{20}+ox^{10}+p)(x^{(\alpha )}+x^{\dfrac {\alpha }{2}}+j)\alpha \in (2^{n})$ Данный ряд сходимости был ещё описан в 19 веке. В теории Галуа рассматриваются подобные многочлены, которые способны оставаться разрешимыми даже при наличии более 5 корней. Основный принцип разрешимости основан на группах подобного уравнения. Коэффициенты располагаются в нём таким образом, что их можно все выразить через другие связки коэффициентов.

Это хорошо видно на простом примере из двух квадратных уравнений.

$(x^{2}+ax+b)(x^{4}+cx^{2}+d)$

После раскрытия которого получаем:

$x^{6}+ax^{5}+(c+b)x^{4}+acx^{3}+(d+bc)x^{2}+adx+bd$

$x^{6}+\omega {_{0}}x^{5}+\omega {_{1}}x^{4}+\omega {_{2}}x^{3}+\omega {_{3}}x^{2}+\omega {_{4}}x+\omega {_{5}}=0$

Можно явно увидеть зависимости нескольких коэффициентов. Например, чтобы найти коэффициент $a$ хватит даже просто значения стоящего перед x^5 т.е. $\omega {_{0}}$

м:

Для коэффициента "c" необходимо $={\dfrac {\omega {_{2}}}{\omega {_{0}}}}$ Зная "a" можем найти ещё "d" ${\dfrac {\omega {_{4}}}{\omega {_{0}}}}$

Коэффициент "b" можно получить 3 различными способами например: $\omega {_{1}}-{\dfrac {\omega {_{2}}}{\omega {_{0}}}}$

Для выражения общей формулы можем воспользоваться готовой формулой для квадратного и Биквадратного уравнения: $x_{1,2}={\dfrac {-\omega {_{0}}\pm {\sqrt {(\omega {_{0}})^{2}-4{\dfrac {\omega {_{1}}\omega {_{0}}-\omega {_{2}}}{\omega {_{0}}}}}}}{2}}$

$x_{1,2,3,4}=\pm {\sqrt {\dfrac {-\omega {_{2}}\pm {\sqrt {\omega {_{0}}(\omega {_{0}}-4\omega {_{4}})}}}{2\omega {_{0}}}}}$

Общий вид с корнями: $\alpha (x-z_{1})(x-z_{2})(x-z_{3})(x-z_{4})(x-z_{5})(x-z_{6})$

• Для трёх скобок, будет аналогичное решение. Также мы работаем с корнями квинтик, имеющих 6 различных вещественных (без учёта 2 симметричных корней) корней и 4 мнимых корня. Или если корни деометральны то 6 мнимых и 4 обычных. Запишем соответствующие скобки:

$(x^{2}+ax+b)(x^{4}+cx^{2}+d)(x^{6}+ex^{3}+f)$ Раскроем скобки:

$x^{12}+ax^{10}+(c+b)x^{10}+(e+ac)x^{9}+(d+ea+bc)x^{8}+(ec+da+eb)x^{7}+(f+eac+bd)x^{6}+(ed+af+ebc)x^{5}+(cf+ead+bf)x^{4}+(acf+ebd)x^{3}+(df+bcf)x^{2}+adfx+bdf$ Скроем коэффициенты:

[Сторона наблюдателя]←→[Сторона составителя] $x^{12}+\omega {_{0}}x^{11}+\omega {_{1}}x^{10}+\omega {_{2}}x^{9}+\omega {_{3}}x^{8}+\omega {_{4}}x^{7}+\omega {_{5}}x^{6}+\omega {_{6}}x^{5}+\omega {_{7}}x^{4}+\omega {_{8}}x^{3}+\omega {_{9}}x^{2}+\omega {_{10}}x+\omega {_{11}}=0$ Также аналогично выражаем буквы:

$a=\omega {_{0}}$

$df={\dfrac {\omega {_{10}}}{\omega {_{0}}}}$

$b={\dfrac {\omega {_{11}}\omega {_{0}}}{\omega {_{10}}}}$

$c=\omega {_{1}}-{\dfrac {\omega {_{11}}\omega {_{0}}}{\omega {_{10}}}}$

$e=\omega {_{2}}-\omega {_{0}}(\omega {_{1}}-{\dfrac {\omega {_{11}}\omega {_{0}}}{\omega {_{10}}}})$

$d'=\omega {_{3}}-ea-bc$

$f={\dfrac {\omega {_{10}}}{\omega {_{0}}d'}}$

Как только мы выразили все коэффициенты, переходим к корням, соответственно:

Все вещественные корни:

$x_{1,2}={\dfrac {-\omega {_{0}}\pm {\sqrt {\omega {_{0}}^{2}-4c'}}}{2}}$

$x_{3,4,5,6}={\sqrt {\dfrac {-c'\pm {\sqrt {c'^{4}-4d'}}}{2}}}$

$x_{7,8}={\sqrt[{3}]{\dfrac {-e\pm {\sqrt {e^{2}-4f}}}{2}}}$

корни с комплексной переменной:

$x=0,5{\sqrt[{3}]{\dfrac {-e\pm {\sqrt {e^{2}-4f}}}{2}}}\pm {\sqrt {3}}{\sqrt[{3}]{\dfrac {-e\pm {\sqrt {e^{4}-4f}}}{2}}}i$

В общем виде это уравнение имеет 6 произвольных корней, что кажется нереальным. Но из-за оссобенных корней группа при изменении остаётся разрешима, сохраняя симметрии.

[Редактирую 4 скобки]

Литература[править]

Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 2003. — 832 с. — 5000 экз. — ISBN 5-8114-0485-9.
Лекция 4 в кн.: Табачников С. Л., Фукс Д. Б. Математический дивертисмент. — М.: МЦНМО, 2011. — 512 с. — 2000 экз. — ISBN 978-5-94057-731-7.